Difference Between Prism and Pyramid: Two Key Shapes of Geometry

The difference between Prism and Pyramid is that a prism features two identical, parallel bases linked by rectangular or parallelogram-shaped faces. In contrast, a pyramid has a single base with triangular faces converging at a point known as the apex.

What is a prism?

A prism is like a 3D shape with two identical bases and flat sides connecting them. These sides are always flat, and the edges are straight, creating a uniform shape. Imagine it as a sandwich with the same filling but in a three-dimensional space. Prisms can have various base shapes, such as triangles or rectangles, and the sides connecting these bases are always perpendicular to the bases. Of course, this unique geometry distinguishes prisms from other 3D shapes.

What is a pyramid?

A pyramid, in contrast, is a unique shape defined by a polygonal base and triangular sides that come together at a single point known as the apex. The base can have various polygonal shapes, but square and triangular bases are the most typical. Think of a pyramid as a building with a pointed roof, like the iconic ancient Egyptian pyramids, which were monumental tombs for pharaohs. This is a key difference between prism and pyramid, as a prism has two parallel identical polygonal bases. In contrast, a pyramid has a single polygonal base with triangular sides converging at the apex.

Difference Between Prism and Pyramid

Prism	Pyramid
A prism has a two-base 3D polyhedron shape.	A pyramid has a single-base 3D polyhedron shape.
It has rectangular-shaped sides.	It has triangular-shaped sides.
The prism’s sides are perpendicular to the base.	The sides of the pyramid are angled with respect to the base.
Prism has no apex to it.	A pyramid has an apex.
Its sides may not always come together at one point.	There’s a point at which its sides come together.
Prism consists of 2 bases.	Pyramids consist of 1 base.
It deals with the fields of geometry and optics.	It deals with the field of geometry only.

Use of Prism

Prisms have versatile applications in everyday life and mathematics. Optics are essential for crafting lenses, such as those in eyeglasses and camera equipment. Prisms are pivotal in constructing modern buildings, especially those featuring glass facades. Additionally, prisms are fundamental in spectroscopy, where they separate and analyze light into its constituent colors, helping us understand the composition of various materials. This is a notable difference between prism and pyramid, as prisms are used in various fields like optics, architecture, and spectroscopy. In contrast, pyramids are typically associated with structures and geometric studies.

Key Properties of Prisms

• Shape: Prisms are three-dimensional shapes with two identical, parallel bases.
• Faces: The sides of a prism are rectangular faces.
• Edges: The lines where the faces meet are called edges.
• Vertices: The points where the edges meet are called vertices.

Use of Pyramid

Undoubtedly, the Pyramids have left an indelible mark on history, most famously associated with the colossal Egyptian pyramids that served as grand tombs for pharaohs. In mathematics and geometry, pyramids are essential for comprehending volume and surface area calculations for various 3D shapes. This highlights a key difference between prisms and pyramids regarding their geometric properties. The difference between prism and pyramid is further emphasized by the pyramid’s distinctive triangular faces and singular apex. It represents a hierarchical management style where decisions flow from the top to the bottom, which mirrors another difference between prism and pyramid, making it a symbolic representation of societal authority and leadership.

Key Properties of Pyramids:

• Base: A pyramid has a polygonal base (like a triangle, square, or pentagon).
• Faces: The sides of a pyramid are triangular faces that converge at a single point called the apex.
• Edges: The lines where the faces meet are called edges.
• Vertices: The points where the edges meet are called vertices.

Similarities Between Prism and Pyramid

1. Both prism and pyramid have three-dimensional shapes.
2. The sides and faces of Prism and Pyramids are Polygon.
3. Both prism and pyramid are part of the polyhedrons category.
4. Prism and Prymid possess no rounded sides, edges, or angles.
5. All sides of the prism and pyramid meet at the bases.
6. Prism and Pyramids are available in a variety of sizes.

Educational Level for Understanding the Difference Between Prism and Pyramid.

The study of prisms and pyramids is typically introduced during middle school or early high school mathematics and geometry courses. Students generally encounter these shapes and their properties in grades 6 to 9, depending on their specific school curriculum and educational system. The difference between prism and pyramid is often one of the first concepts that students explore when learning about 3-D shapes.

Thus, concepts related to prisms and pyramids, including the key differences between prism and pyramid structures, continue to be explored in more advanced math courses as students progress. Understanding the difference between prism and pyramid is foundational for later studying more complex geometric topics.

Application of Prisms

Prisms are incredibly versatile geometric shapes with many practical applications in various fields. Let’s delve further into the multiple applications of prisms:

1. Optics: Of course, pyramids can bend and redirect light, essential for correcting vision problems, capturing clear images, or magnifying distant objects.

2. Architecture: Prisms play a significant role in the architectural world. They are used in the construction of modern buildings with glass facades. By incorporating colorful elements into the architectural design, architects can ensure the even distribution of natural light throughout the interior spaces. This enhances aesthetics and reduces the need for artificial lighting, making structures more energy-efficient.

3. Spectroscopy: Prisms are indispensable tools in spectroscopy. They separate white light into constituent colors, forming a spectrum.

Application of Pyramids

Pyramids have played a significant role in both historical and modern contexts, with diverse applications:

1. Historical Monuments: The most iconic use of pyramids is as historical monuments. Ancient civilizations, most notably the Egyptians, constructed grand pyramid-shaped tombs for pharaohs and rulers. These structures continue to captivate the imagination and are enduring symbols of human achievement and engineering prowess.

2. Geometry and Mathematics: Pyramids are fundamental in mathematics and geometry education. They are essential tools for teaching concepts related to three-dimensional shapes, surface area, and volume calculations. Students can comprehend and manipulate pyramids as they progress through their math curriculum.

3. Organizational Structure: The concept of a pyramid applies not only to geometry but also describes how organizations organize themselves. A “pyramid structure” signifies a well-defined hierarchy in the business realm, with decision-making and authority originating from the top and cascading through various levels. It reflects the chain of command in many corporate organizations.

Students typically encounter a difference between prism and pyramid in middle or early high school mathematics and geometry courses. Understanding the difference between prism and pyramid is often one of the first steps in learning about 3D shapes. The specific grade level may vary depending on the educational system and curriculum. Studying these shapes and the key difference between prism and pyramid often continues in more advanced math courses as students progress in their mathematical education.

What are the different types of Prism and Pyramid?

Let’s delve further into the various types of prisms and pyramids:

Types of Prisms

1. Triangular Prism (Has Triangular Bases): This prism type has a constant cross-section, and its sides are always flat.
2. Square Prism (Has Square Bases): The sides of this prism are perpendicular to the bases, making it a popular choice in engineering and architecture.
3. Rectangular Prism (Has Rectangular Bases): A rectangular prism has two rectangular bases and four rectangular faces connecting them. A familiar shape, often observed in everyday objects like boxes, features a practical design due to its uniform sides.
4. Pentagonal Prism (Has Pentagonal Bases): Two pentagonal bases and five connecting faces, either rectangular or parallelogram, characterize a pentagonal prism. Its uniqueness lies in the pentagonal shape of its bases.
5. Hexagonal Prism (Has Hexagonal Bases): A hexagonal prism has two hexagonal bases and six rectangular or parallelogram faces connecting them. This shape generally showcases the hexagon, a polygon with six sides.

Types of Pyramids

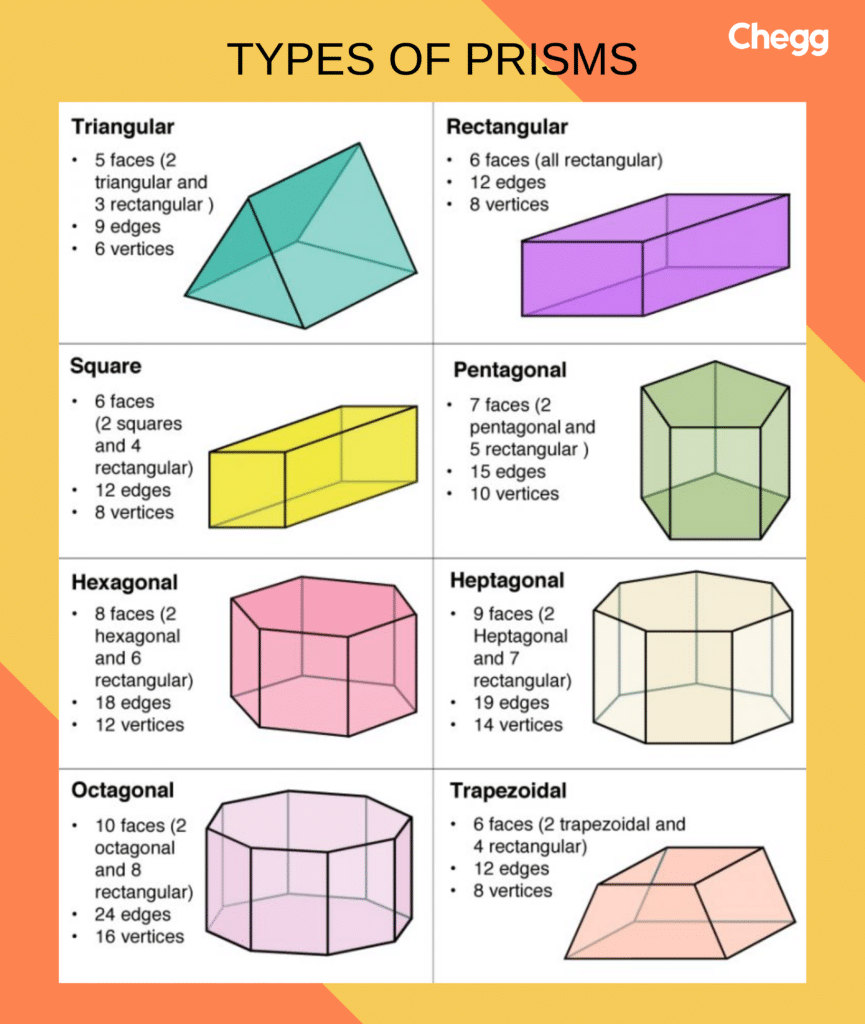
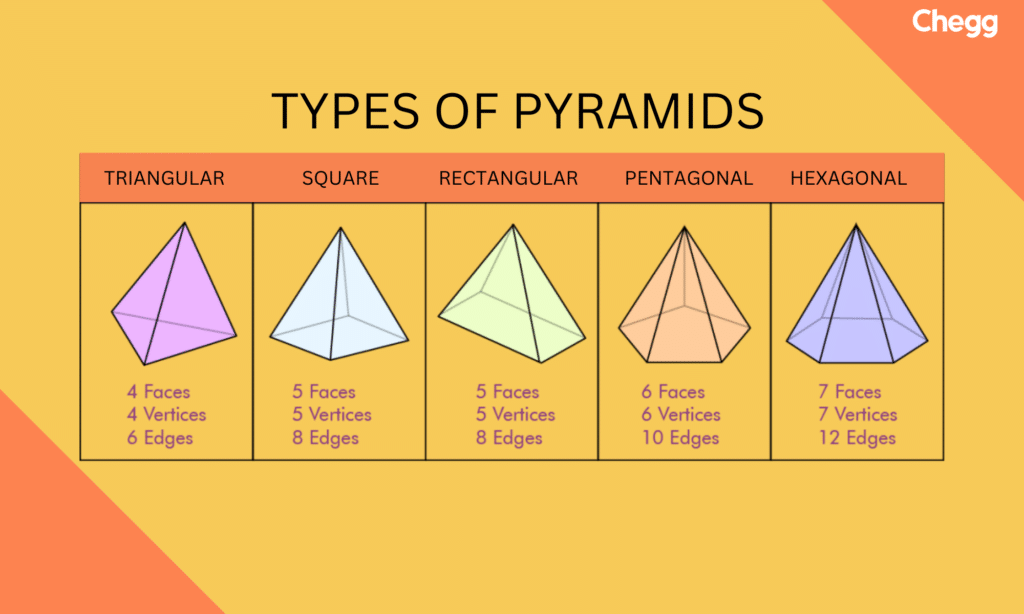
Pyramids also come in different types, depending on the shape of their base:

1. Triangular Pyramid (Has a Triangle as Its Base): A triangular pyramid features a triangular base, and consequently, three triangular faces meet at a single point, forming the apex.
2. Square Pyramid (has a square as its base): A square pyramid features a square base with four triangular faces converging at a central apex.
3. Pentagonal Pyramid (has a Pentagon as its base): A pentagonal pyramid has a five-sided base. Thus forming a pentagon. Similarly, this pyramid type has five triangular faces colliding at the uppermost point. We know that point as the apex.
4. Right Pyramid: In a right pyramid, the apex is positioned directly above the center of the base. This creates a symmetrical structure. The height of a right pyramid is the vertical distance measured from the apex to the center of the base.

Also read:

• Difference Between England and Britain: An Overview
• Meaning of Gen Z The Enigmatic Generation Shaping the Future
• National Mathematics Day 2023: Understanding Themes & History
• The Ecological Pyramid

Formulas for Prisms and Pyramids?

What is the difference between Prism and Pyramid?

Let’s look at the prism and pyramid differences in the following table:

Characteristics	Prism	Pyramid
Number of Faces	Prisms have two identical polygonal bases and rectangular or parallelogram faces connecting them.	Pyramids have one polygonal base and triangular faces that converge at an apex.
Surface Area Formula	2B + Ph, where B = the area of the base,P = the perimeter of the base, and h = the height of the prism.	(1/2)Pl + B, where P = perimeter of the base, l = slant height, and B = area of the base.
Volume Formula	The formula for the volume of a prism is Bh, where B = area of the base and h = height of the prism.	Pyramids are used for pointy, iconic architectural designs like steeples or pyramid-shaped roofs.
Symmetry	Prisms are generally symmetrical along their central axis, with the apex directly above the center of the base.	Pyramids have a single apex, and their symmetry depends on the shape of the base.
Common Objects	Everyday objects like rectangular boxes, cuboids, and some buildings are prisms.	Historical monuments like the Egyptian pyramids, triangular roofs, and certain buildings are pyramids.
Architectural Use	Prisms are used in structures with even cross-sections along their length, often with glass facades for natural light.	Pyramids are used for pointy, iconic architectural designs, such as steeples or pyramid-shaped roofs.
Hierarchical Structure	The term “pyramid structure” is often used to describe organizational hierarchies with a top-down decision-making flow.	No similar organizational term is associated with prisms.
Popular Shapes	Triangular, square, and rectangular prisms are common shapes.	Square and triangular pyramids are well-known shapes.

Common Properties of Prism and Pyramid

Despite the difference between prism and pyramid, there are some similarities between prisms and pyramids share some key features:

• Polygonal Bases: Both rest on flat, multi-sided bases (triangles, squares, etc.).
• Flat Faces: Their sides are made up of flat surfaces.
• Building Blocks: Faces, edges, and vertices combine to form these 3D shapes. (Faces: flat surfaces, Edges: where faces meet, Vertices: corners where edges meet).

Prism vs Pyramid

A prism and a pyramid are two distinct three-dimensional geometric shapes, and understanding the difference between them is essential in geometry. A pyramid is not a prism; it has one base with triangular sides meeting at an apex. In contrast, a prism has two parallel bases connected by rectangular or parallelogram sides.

1. Base Shapes

Prisms have two parallel and identical polygonal bases (such as triangles, squares, or rectangles) connected by rectangular or parallelogram sides. This is one key difference between a prism and a pyramid. On the other hand, pyramids have only one polygonal base (triangle, square, pentagon, etc.), from which triangular faces converge at a single point called the apex. This distinction further highlights the difference between prism and pyramid in their structure and shape.

2. Number of Bases

• Prism: Prisms have two bases, which makes them bi-pyramidal.
• Pyramid: Pyramids have a single base, giving them their characteristic pointy shape with one apex.

3. Faces

• Prism: Prisms typically have rectangular or parallelogram faces between the bases and the bases themselves.
• Pyramid: Pyramids have triangular faces that meet at the apex.

4. Symmetry

• Prism: Prisms often exhibit symmetry along their central axis, with the apex directly above the center of the base.
• Pyramid: Pyramids may have rotational symmetry based on the shape of their base but do not have a central axis of symmetry.

In summary, prisms have identical bases and rectangular sides, whereas pyramids have single bases and triangular sides converging at an apex. These differences in base shapes, cross-sections, and faces are critical distinctions between these fundamental geometric shapes, further emphasizing the difference between prism and pyramid in geometry.

Prism and Pyramid differ primarily in their shape and volume formulas. Prisms have a consistent cross-sectional shape, and their volume can be calculated by multiplying the base area by the height. Pyramids have different cross-sectional shapes that taper towards the apex. The location of the base of a pyramid is multiplied by one-third of the height to determine its volume.

• A prism consists of two parts: a base and a translated copy joined by parallelograms or rectangular faces, while a pyramid consists of a base and a vertex joined by triangular faces.
• The faces typically form parallelograms in a prism, but the faces are always triangles in a pyramid.
• A prism is generally defined as a transparent object that can split, reflect, or refract light, whereas a pyramid is usually connected to a solid structure.

Difference Between Prism and Pyramid: Solved Examples

1. Shape with a Square Base and Four Triangular Faces:
   • Question: A 3D shape has a square base and four triangular faces that converge at a common vertex. Is it a prism or a pyramid?
   • Solution: This shape is a pyramid because it has a square base and triangular faces that meet at a single vertex.
2. Shape with a Rectangular Base and Parallelogram Lateral Faces:
   • Question: A 3D shape has a rectangular base, and its lateral faces are parallelograms. Is it a prism or a pyramid?
   • Solution: This shape is a prism because it has a rectangular base and parallelogram lateral faces.
3. Shape with a Hexagonal Base and Six Triangular Faces:
   • Question: A 3D shape has a hexagonal base and six triangular faces that converge at a common vertex. Is it a prism or a pyramid?
   • Solution: This shape is a pyramid because it has a hexagonal base and triangular faces that meet at a single vertex.
4. Shape with a Pentagonal Base and Rectangular Lateral Faces:
   • Question: A 3D shape has a pentagonal base, and its lateral faces are rectangles. Is it a prism or a pyramid?
   • Solution: This shape is a prism because it has a pentagonal base and rectangular lateral faces.

Conclusion: Difference Between Prism and Pyramid

The key difference between prism and pyramid lies in their geometry and structure. Prisms have two congruent and parallel bases, while pyramids have a polygonal base with triangular sides converging at a single apex. This fundamental difference results in unique geometric characteristics and shapes for each. Prisms maintain uniform cross-sections throughout their length, whereas pyramids have a single point where all sides meet.

These difference between prism and pyramid have implications for their volume, surface area, and applications in various fields, such as mathematics, engineering, and architecture. Understanding these disparities is essential for effectively working with and difference between prism and pyramid in different contexts.

Frequently Aksed Questions(FAQs)