आर्यभट्ट : आर्यभट्ट कौन थे? जानिए सम्पूर्ण परिचय 

आर्यभट्ट, प्राचीन भारत के महान गणितज्ञ और खगोलशास्त्री, का जन्म 476 ईस्वी में हुआ था। उन्होंने केवल 23 वर्ष की आयु में ‘आर्यभटीय’ नामक ग्रंथ की रचना की, जिसमें गणित और खगोल विज्ञान के कई महत्वपूर्ण सिद्धांत प्रस्तुत किए गए हैं। आर्यभट्ट ने पाई (pi/ π ) का सटीक मान 3.1416 निकाला और त्रिकोणमिति में साइन (ज्या) की अवधारणा को विकसित किया। उन्होंने पृथ्वी की परिधि का भी सटीक अनुमान लगाया और ग्रहों की गति के सिद्धांतों को समझाया। उनकी गणनाओं और सिद्धांतों ने न केवल भारतीय विज्ञान को समृद्ध किया, बल्कि विश्वभर के वैज्ञानिकों को भी प्रेरित किया। आर्यभट्ट का योगदान आज भी विज्ञान और गणित के क्षेत्र में अमूल्य माना जाता है।

क्या आप उनके किसी विशेष योगदान के बारे में और जानना चाहेंगे?

आर्यभट्ट कौन थे?

आर्यभट्ट एक महान भारतीय गणितज्ञ और खगोलशास्त्री थे जिन्होंने 5वीं शताब्दी में महत्वपूर्ण भूमिका निभाई थी। उनका जन्म कुसुमपुर (आज का पटना) में हुआ था और वे नालंदा विश्वविद्यालय में शिक्षित हुए थे।

उन्होंने  खगोल विज्ञान और गणित में क्रांतिकारी योगदान दिया। उनकी सबसे प्रसिद्ध कृति “आर्यभटीय” है, जिसमें उन्होंने ग्रहों की गति, ग्रहण, और ऋतुओं के बारे में अपने विचारों का वर्णन किया है। 

आर्यभट्ट का जन्म कब हुआ?

आर्यभट्ट का जन्म स्थान

आर्यभट्ट का जन्म 476 ईस्वी में हुआ था। उनकी जन्मस्थली मगध (आज का बिहार) मानी जाती है। आर्यभट ने आर्यभटीय में उल्लेख करते हुए खुदको कुसुमपुर (आज का पटना) का निवासी बताया है। लेकिन, कुछ इतिहासकारों का मानना है कि उनका जन्म लल्लक (आज का गया) में हुआ था। 

उनकी जन्म तिथि को लेकर कुछ मतभेद हैं, लेकिन अधिकांश इतिहासकार 476 ईस्वी को स्वीकार करते हैं।

शिक्षा और प्रारंभिक जीवन

आर्यभट्ट का प्रारंभिक जीवन और शिक्षा बहुत रोचक और प्रेरणादायक रहा। यह माना जाता है कि उन्होंने अपने पिता, जो एक गणितज्ञ और खगोलशास्त्री थें, उनसे ही अपनी प्रारंभिक शिक्षा पटना में प्राप्त की थी।

आर्यभट्ट ने बाद में तक्षशिला और नालंदा जैसे प्रसिद्ध विश्वविद्यालयों में अध्ययन किया, जहां उन्होंने खगोलशास्त्र, गणित और विज्ञान में विशेष ज्ञान प्राप्त किया। उनकी शिक्षा में गणित और खगोलशास्त्र का विशेष स्थान था, और इन विषयों पर उनका योगदान अत्यंत महत्वपूर्ण रहा।

आर्यभट्ट के कार्य और उपलब्धियाँ

आर्यभट्ट के कार्य और उपलब्धियाँ अनेक हैं। उन्होंने अपने गणित और खगोल विज्ञान की बेहतरीन समझ से इन विषयों पर अपना महत्वपूर्ण योगदान दिया। जिसमें: 

1. शून्य की अवधारणा, 
2. संख्याओं का वर्गमूल और घनमूल, 
3. त्रिकोणमिति, 
4. पृथ्वी की परिधि का मापन, 
5. पृथ्वी का घूर्णन, 
6. ग्रहण की व्याख्या, जैसे और भी तथ्य सामिल थें।

आर्यभट्ट का गणित में योगदान

शून्य का उपयोग 

आर्यभट्ट को शून्य की खोज का श्रेय दिया जाता है, जिन्होंने इसे संख्या प्रणाली में शामिल किया। आर्यभट्ट ने गणित में शून्य के महत्व को समझाया और इसके उपयोग को प्रचलित किया। 

यह एक महत्वपूर्ण क्रांतिकारी बदलाव था, क्योंकि इससे पहले, भारतीय गणित में शून्य की अवधारणा नहीं थी। उन्होंने शून्य को केवल एक खाली जगह के रूप में नहीं, बल्कि एक संख्या के रूप में भी परिभाषित किया। 

उन्होंने ऋणात्मक संख्याओं का भी उपयोग किया, जो उस समय गणित में एक और नया विचार था। आज शून्य का उपयोग स्थानीय मान प्रणाली, ऋणात्मक संख्याएं, अलजेब्रा, खगोल विज्ञान जैसी कई विषयों में किया जा रहा है।

दशमलव पद्धति

उनकी रचना “आर्यभट्टीय” में दशमलव संख्या प्रणाली का उल्लेख मिलता है, जिसमें उन्होंने संख्याओं को लिखने के लिए दस अंकों (0 से 9) का प्रयोग किया था। उन्होंने शून्य (0) को भी एक अंक के रूप में स्वीकार किया और इसका प्रयोग संख्याओं को लिखने में किया।

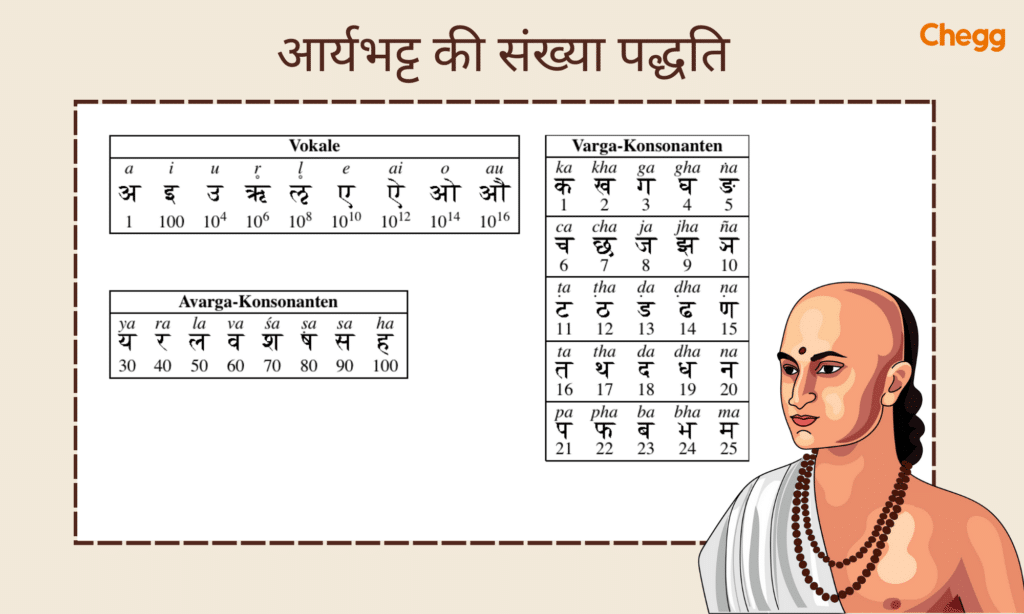
आर्यभट्ट ने दशमलव संख्याओं के साथ गणना करने के लिए भी कई तरीके विकसित किए, जैसे कि जोड़, घटाव, गुणा और भाग। उन्होंने वर्गमूल और घनमूल निकालने के लिए भी दशमलव पद्धति का उपयोग किया।

आर्यभट्ट के योगदान ने दशमलव पद्धति को भारत में लोकप्रिय बनाने में महत्वपूर्ण भूमिका निभाई। यह प्रणाली बाद में अरबों द्वारा अपनाई गई और 10वीं शताब्दी तक यूरोप में भी फैल गई। आज, दशमलव पद्धति दुनिया भर में सबसे अधिक इस्तेमाल होने वाली संख्या प्रणाली है।

त्रिकोणमिति

आर्यभट्ट का योगदान त्रिकोणमिति को एक विकसित गणितीय विषय के रूप में स्थापित करने में बहुत महत्वपूर्ण रहा। उनकी रचना “आर्यभट्टीय” में त्रिकोणमिति के कई महत्वपूर्ण अवधारणाओं का उल्लेख मिलता है, जिनमें शामिल हैं:

1. ज्या (sine): किसी समकोण त्रिभुज में आधार के लम्ब की परिक्रमा का अनुपात कर्ण से।
2. कोज्या (cosine): किसी समकोण त्रिभुज में आधार की परिक्रमा का अनुपात कर्ण से।
3. उत्क्रम ज्या (versine): ज्या का उत्क्रम।
4. व्युज्या (inverse sine): ज्या का व्युत्क्रम।

आर्यभट्ट ने त्रिकोणों को हल करने के लिए कई सूत्र भी विकसित किए, जिनमें ज्या-ज्या सूत्र और कोज्या-कोज्या सूत्र शामिल हैं। उन्होंने त्रिभुजों के क्षेत्रफल और परिमाप की गणना के लिए भी तरीके विकसित किए।

उनकी रचना “आर्यभट्टीय” में साइन (ज्या)  फलों की एक तालिका शामिल है, जिसे “आर्यभट्ट की साइन तालिका” के नाम से जाना जाता है। यह तालिका 0 से 90 डिग्री तक के कोणों के लिए साइन फल प्रदान करती है। उन्हों ने साइन फल निकालने के लिए एक नई विधि विकसित की, जिसे अंतर विधि कहा जाता है। यह विधि पिछले कोणों के साइन फल का उपयोग करके अगले कोण का साइन फल निकालने पर आधारित है। इसे इस तालिका से समझते हैं:

क्रम सं०	(A) कोण का मान (डिग्री, आर्कमिनट में )	आर्यभट्ट द्वारासंख्यात्मक संकेतन में मान (देवनागरीमें)	आर्यभट्ट के अनुसार ‘ज्य’ का मान	ज्या का आधुनिक मान (3438 × sin (A) के अनुसार)
1	3° 45’	मखी	225′	224.8560
2	7° 30’	भखि	449′	448.7490
3	11° 15’	फ़ख़ि	671′	670.7205
4	15° 00’	ढखी	890′	889.8199
5	18° 45’	आँखि	1105′	1105.1089
6	22° 30’	धिंखी	1315′	1315.6656
7	26° 15’	ङखी	1520′	1520.5885
8	30° 00’	हस्ज़	1719′	1719.0000
9	33° 45’	स्की	1910′	1910.0505
10	37° 30’	किश्ग	2093′	2092.9218
11	41° 15’	शघकी	2267′	2266.8309
12	45° 00’	किघ्व	2431′	2431.0331
13	48° 45’	घ्लकी	2585′	2584.8253
14	52° 30’	किग्र	2728′	2727.5488
15	56° 15’	हक्य	2859′	2858.5925
16	60° 00’	ढकी	2978′	2977.3953
17	63° 45’	किच	3084′	3083.4485
18	67° 30’	एसजी	3177′	3176.2978
19	71° 15’	झश	3256′	3255.5458
20	75° 00’	ङ्व	3321′	3320.8530
21	78° 45’	क्	3372′	3371.9398
22	82° 30’	प	3409′	3408.5874
23	86° 15’	एफ	3431′	3430.6390
24	90° 00’	छ	3438′	3438.0000

अंकगणित

आर्यभट्ट का योगदान अंकगणित में बहुत महत्वपूर्ण और क्रांतिकारी रहा है। उन्होंने गणित को नए दृष्टिकोण से देखा और कई महत्वपूर्ण सिद्धांतों और तकनीकों का विकास किया। जिसमें शून्य की अवधारणा, संख्याओं का वर्गमूल और घनमूल, दशमलव पद्धति, एकल चर द्विघात समीकरण का समाधान, दशमलव स्थानों तक π का ​​मान, आदि सामिल हैं। आज भी कई विशेषज्ञ आर्यभट्ट का गणित में योगदान की सराहना करते हैं और उनके दिए गए नियमों की मदद लेते हैं। 

आर्यभट का गणित में योगदान सर्वोपरि रहा है, इसलिए उन्हें भारतीय गणित के पिता (Father of Indian Mathematician) भी कहा जाता है।

आर्यभट्ट का योगदान खगोलशास्त्र में 

पृथ्वी की घूर्णन गति

पहले वैज्ञानिकों में से एक थे जिन्होंने यह माना था कि पृथ्वी अपनी धुरी पर घूमती है। उन्होंने अपनी रचना “आर्यभट्टीय” में इस विचार का उल्लेख किया था, जो 499 ईस्वी में लिखी गई थी। उस समय, यह व्यापक रूप से माना जाता था कि पृथ्वी स्थिर है और आकाश घूमता है। उनके इस विचार को क्रांतिकारी माना जाता था, और इसे वैज्ञानिक समुदाय में काफी विरोध का सामना करना पड़ा। 

आर्यभट्ट के तर्क:

1. तारों की गति: यदि पृथ्वी घूमती नहीं है, तो तारे पूर्व से पश्चिम की ओर गति करने चाहिए। लेकिन, हम देखते हैं कि कुछ तारे पूर्व की ओर गति करते हैं, जबकि कुछ पश्चिम की ओर गति करते हैं। यह तभी संभव है जब पृथ्वी अपनी धुरी पर घूम रही हो।
2. दिन और रात: यदि पृथ्वी घूमती नहीं है, तो पृथ्वी के सभी हिस्सों पर दिन और रात एक साथ होंगे। लेकिन, हम देखते हैं कि पृथ्वी के कुछ हिस्सों में दिन होता है, जबकि अन्य में रात होती है। यह तभी संभव है जब पृथ्वी अपनी धुरी पर घूम रही हो।
3. गिरते हुए पिंड: यदि पृथ्वी घूमती नहीं है, तो गिरते हुए पिंड पृथ्वी के पूर्वी भाग में पश्चिम की ओर गिरेंगे। लेकिन, हम देखते हैं कि गिरते हुए पिंड पृथ्वी के केंद्र की ओर गिरते हैं। यह तभी संभव है जब पृथ्वी अपनी धुरी पर घूम रही हो।

सौरमंडल

सूर्यमंडल को समझने में आर्यभट्ट का योगदान बेहद महत्वपूर्ण और अद्वितीय रहा है। उनके समय में, खगोलशास्त्र को समझने के तरीके काफी सीमित थे, लेकिन उन्होंने  ने अपनी गहरी वैज्ञानिक दृष्टि और गणनाओं से कई महत्वपूर्ण सिद्धांत प्रस्तुत किए। आइए उनके प्रमुख योगदानों पर नजर डालते हैं:

1. पृथ्वी का घूर्णन: आर्यभट्ट ने यह बताया कि पृथ्वी अपनी धुरी पर घूमती है, जिससे दिन और रात होते हैं। यह एक क्रांतिकारी विचार था, क्योंकि उस समय यह माना जाता था कि सूर्य पृथ्वी के चारों ओर घूमता है।
2. ग्रहों की गति: उन्होंने  ने ग्रहों की गति का अध्ययन किया और उनके कक्षाओं की गणना की। उन्होंने बताया कि ग्रह अंडाकार (elliptical) कक्षाओं में चलते हैं, और उनकी गति सूर्य के चारों ओर होती है।
3. पृथ्वी की परिधि का मापन: आर्यभट्ट ने पृथ्वी की परिधि का सटीक मापन किया। उनकी गणनाओं ने यह साबित किया कि पृथ्वी गोलाकार है और उसकी परिधि लगभग 39,968 किलोमीटर है, जो कि वास्तविक परिधि 40,075 के बहुत करीब है।
4. खगोलीय घटनाओं की भविष्यवाणी: उन्होंने खगोलीय घटनाओं की भविष्यवाणी करने की तकनीकें विकसित कीं। उन्होंने ग्रहों की स्थितियों और उनके संक्रमण (transits) का सटीक वर्णन किया, जिससे खगोलशास्त्र में नए आयाम जुड़े।

सौर और चंद्र ग्रहण

आर्यभट्ट का सौर और चंद्र ग्रहण को समझने में बहुत महत्वपूर्ण योगदान रहा है। उनके समय में, ग्रहणों के बारे में कई मिथक और गलत धारणाएँ थीं, लेकिन उन्होंने वैज्ञानिक दृष्टिकोण से इन खगोलीय घटनाओं को समझाया। आइए उनके प्रमुख योगदानों पर नजर डालें:

1. वैज्ञानिक दृष्टिकोण: आर्यभट्ट ने सौर और चंद्र ग्रहण को खगोलीय घटनाओं के रूप में समझाया, जो पृथ्वी, सूर्य और चंद्रमा की स्थितियों के कारण होते हैं।
2. चंद्र ग्रहण: उन्होंने बताया कि चंद्र ग्रहण तब होता है जब पृथ्वी, सूर्य और चंद्रमा के बीच आ जाती है, और पृथ्वी की छाया चंद्रमा पर पड़ती है। उन्होंने यह समझाया कि यह घटना चंद्रमा के पूर्णिमा के समय होती है।
3. सौर ग्रहण: उन्होंने यह भी स्पष्ट किया कि सौर ग्रहण तब होता है जब चंद्रमा, पृथ्वी और सूर्य के बीच आ जाता है, जिससे सूर्य का प्रकाश पृथ्वी पर पूरी तरह या आंशिक रूप से नहीं पहुंच पाता। यह घटना अमावस्या के समय होती है।
4. ग्रहण की गणना: आर्यभट्ट ने ग्रहणों की सटीक गणना के तरीके विकसित किए। उन्होंने ग्रहण के समय और उसकी अवधि की गणना के लिए विधियाँ बताईं।
5. ग्रंथ ‘आर्यभटीय’: उन्होंने अपने प्रसिद्ध ग्रंथ ‘आर्यभटीय’ में सौर और चंद्र ग्रहणों के सिद्धांतों को विस्तार से समझाया। उनका ये ग्रंथ आने वाली पीढ़ियों के लिए मार्गदर्शक बना।

आर्यभट्ट की विरासत

शिक्षा और अनुसंधान

• शिक्षा प्रणाली: उनकी शिक्षण विधियों ने बाद के वैज्ञानिकों को प्रेरित किया और भारत में शिक्षा प्रणाली को विकसित करने में मदद की।
• विज्ञान और गणित: उनके गणितीय और खगोलीय खोजों ने वैज्ञानिक क्रांति में योगदान दिया और आधुनिक विज्ञान और गणित की नींव रखी।
• भारतीय संस्कृति: उन्होंने भारतीय संस्कृति और ज्ञान को समृद्ध किया और भारत को दुनिया के एक प्रमुख ज्ञान केंद्र के रूप में स्थापित करने में मदद की।
• नालंदा विश्वविद्यालय: आर्यभट्ट ने अपने जीवन का एक महत्वपूर्ण हिस्सा नालंदा विश्वविद्यालय में शिक्षा और अनुसंधान में बिताया।
• ज्ञान का प्रसार: उन्होंने विभिन्न विषयों जैसे गणित, खगोल विज्ञान, ज्योतिष और आयुर्वेद में ज्ञान का प्रसार किया।
• शिक्षण विधियाँ: उन्होंने नए शिक्षण विधियों का विकास किया और छात्रों को प्रेरित करने के लिए रचनात्मक तरीकों का उपयोग किया।

सम्मान

1. भारत सरकार ने आर्यभट्ट के सम्मान में अपने पहले उपग्रह का नाम आर्यभट्ट (1975 में प्रक्षेपित) रखा था।
2. आर्यभट्ट के सम्मान में बिहार सरकार द्वारा 2010 में आर्यभट्ट ज्ञान विश्वविद्यालय (AKU), पटना की स्थापना की गई।
3. आर्यभट्ट के सम्मान में 1988 में अंतर विश्वविद्यालय खगोल विज्ञान और खगोल भौतिकी केंद्र ( IUCAA ), पुणे के परिसर में उनकी की प्रतिमा की स्थापना की गई।
4. उनके जीवन और कार्यों पर कई किताबें और लेख लिखे गए हैं।
5. उन्हें दुनिया भर के वैज्ञानिकों और गणितज्ञों द्वारा एक प्रतिभाशाली और अभिनव विचारक के रूप में सम्मानित किया जाता है।
6. उनके कार्यों का कई भाषाओं में अनुवाद किया गया है और उनका अध्ययन दुनिया भर के विश्वविद्यालयों में किया जाता है।

Please read: सूरदास का जीवन परिचय

आर्यभट्ट के प्रमुख ग्रंथ

आर्यभटीय

“आर्यभटीय” आर्यभट्ट द्वारा रचित एक महत्वपूर्ण ग्रंथ है, जिसमें गणित और खगोलशास्त्र के सिद्धांत शामिल हैं। यह चार खंडों में विभाजित है: दशगीतिका, गणितपाद, कालक्रियापाद, और गोलपाद। इसमें त्रिकोणमिति, ज्या (साइन) तालिका, ग्रहणों की गणना, और पृथ्वी के घूर्णन जैसी अवधारणाओं की चर्चा की गई है। ये ग्रंथ उन्होंने 499 ईस्वी में लिखा था जब वो केवल 23 साल के थे। ‘आर्यभटीय’ ने न केवल भारतीय गणित को समृद्ध किया, बल्कि वैश्विक वैज्ञानिक समुदाय को भी प्रेरित किया।

दशगीतिका

“दशगीतिका” में खगोलशास्त्र और गणित के प्रमुख सिद्धांतों का वर्णन है। यह ग्रंथ दस छंदों (गीतिका) में विभाजित है, जिनमें समय की गणना, ग्रहों की गति, और त्रिकोणमिति के सिद्धांत शामिल हैं। “दशगीतिका” ने आर्यभट्ट के ज्ञान और वैज्ञानिक दृष्टिकोण को सरल और संक्षिप्त रूप में प्रस्तुत किया, जो उस समय के खगोलविदों और गणितज्ञों के लिए बहुत उपयोगी साबित हुआ। आज भी इस ग्रंथ को विशेषज्ञों द्वारा पढ़ा जाता है।

निष्कर्ष

आर्यभट्ट का जीवन परिचय हमें यह सिखाता है कि ज्ञान और अनुसंधान की कोई सीमा नहीं होती। उनके योगदान ने न केवल भारतीय गणित और खगोल विज्ञान को समृद्ध किया, बल्कि विश्व भर में वैज्ञानिक सोच और समझ को नई ऊंचाइयों पर पहुँचाया। आर्यभट्ट की शिक्षा की विशेषता यह थी कि उन्होंने केवल पारंपरिक शिक्षाओं को ही नहीं अपनाया, बल्कि नए विचारों और सिद्धांतों को भी विकसित किया। उनके विचार और सिद्धांत आज भी उपयुक्त हैं और हमारे जीवन को प्रेरित करते हैं। 

इस ब्लॉग में आपने आर्यभट्ट कौन थे, उनका जन्म स्थान, जीवन परिचय, उनके कार्य और उपलब्धियाँ, उनका गणित तथा खगोलशास्त्र में योगदान, उनकी विराशात और आर्यभट्ट के प्रमुख ग्रंथ के बारे में गहराई से जाना।

अक्सर पूछे जाने वाले प्रश्न (FAQs)